Le logarithme d'une puissance : log b ( M p ) = p log b ( M ) \log_b(M^p)=p\log_b(M) logb(Mp)=plogb(M) Le logarithme d'une puissance est le produit de l'exposant par le logarithme de la base. Voir un exemple numérique. On utilise cette propriété pour manipuler les expressions logarithmiques. Quel est le logarithme décimal de 000-1 ? On écrit : log 0,001 = -3 ; log 0,1 = -1 ; log 10 = 1 ; log 1000 = 3 etc. log 10 a = a Pour trouver le logarithme décimal de tout nombre positif, on utilise la touche log de la calculatrice. Remarque : log 1 = 0 ; log 10 = 1 ; log 100 = 2 : le log d'un nombre supérieur à 1 est positif.
Comment enlever log 10 ?
Si ma mémoire reste bonne, l'inverse de log10(X) c'est 10^(X) (10 exposant X). A+.
Comment résoudre e x 0 ? On sait que eA > pour tout A réel, donc l'équation ex + e-x = n'a pas de solution, puisque la somme de deux quantités strictement positives ne peut être nulle. D'où : S = ∅ . Pas de problème de domaine de définition ( -x + 4 et -x toujours calculables).
Comment passe de la forme log à exponentielle ?
- ln() et exp() sont des fonctions réciproques l'une de l'autre. ln(ex) = eln(x) = x. 10 = eln(10) => 10x = [eln(10)]x = ex ln(10) log10(10x) = 10log10(x) = x. 10log10(e) = e. ...
- ou bien : y = 10x => ln(y) = ln(10x) = x ln(10) => eln(y) = y = 10x = ex ln(10) y = ex
Pourquoi avoir inventé ln ? Ces tables de correspondances ont été créées initialement pour simplifier les calculs trigonométriques apparaissant dans les calculs astronomiques et seront utilisées quelques années plus tard par Kepler.
Quelles sont les propriétés de l'exponentielle ?
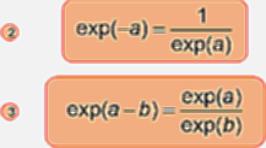
La fonction exponentielle est strictement croissante et continue sur R donc, d'après le théorème de la bijection : elle réalise une bijection de R sur exp(R) . signifie que pour tout réel y > 0, il existe un et un seul x réel tel que y = exp(x).